편집 요약 없음 |
편집 요약 없음 |
||
| (같은 사용자의 중간 판 2개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
==개요== | ==개요== | ||
오일러 지표(Euler characteristic)은 [[위상수학]]적 [[상수(常數)]]라고 할 수 있는데, 다면체 쪽에 국한 한다면 V-E+F 값이 오일러 지표가 되고, 이 값은 일정하다. | [[오일러]] 지표(Euler characteristic)은 [[위상수학]]적 [[상수(常數)]]라고 할 수 있는데, 다면체 쪽에 국한 한다면 V-E+F 값이 오일러 지표가 되고, 이 값은 일정하다. | ||
<br> | <br> | ||
<br> | <br> | ||
| 37번째 줄: | 37번째 줄: | ||
[[파일:V-e%2Bf%3D2_2.jpg]]<p> | [[파일:V-e%2Bf%3D2_2.jpg]]<p> | ||
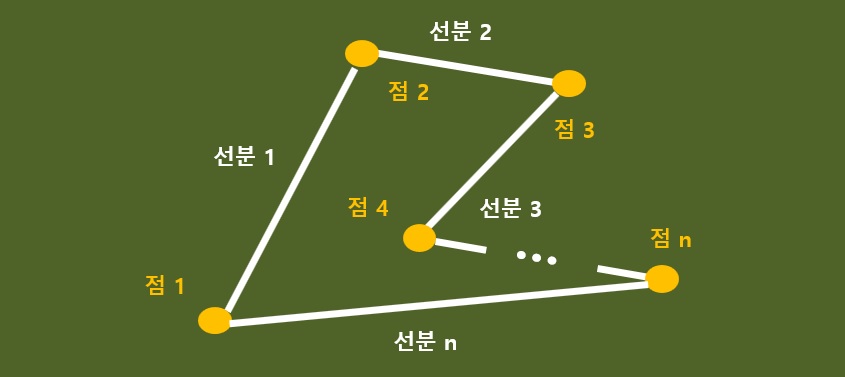
위 선을 링 처럼 만들면 갯수차이가 없다<br> | 위 선을 링(ring) 처럼 만들면 갯수차이가 없다<br> | ||
<br> | <br> | ||
<br> | <br> | ||
| 65번째 줄: | 65번째 줄: | ||
[[파일:V-e%2Bf%3D2_6.jpg]]<p> | [[파일:V-e%2Bf%3D2_6.jpg]]<p> | ||
저런 면을 점과 선, 면의 변화 없이 저런 바구니 형태로 만들 수 있다<br> | 저런 면을 점과 선, 면의 갯수 변화 없이 저런 바구니 형태로 만들 수 있다<br> | ||
<br> | <br> | ||
<br> | <br> | ||
| 80번째 줄: | 80번째 줄: | ||
자세한 내용은 아래 영상을 보시고 참고하시면 되겠습니다.<br> | '''<big>자세한 내용은 아래 영상을 보시고 참고하시면 되겠습니다.</big>'''<br> | ||
<br> | |||
2019년 8월 13일 (화) 16:38 기준 최신판
개요
오일러 지표(Euler characteristic)은 위상수학적 상수(常數)라고 할 수 있는데, 다면체 쪽에 국한 한다면 V-E+F 값이 오일러 지표가 되고, 이 값은 일정하다.
다면체에서의 공식
설명
V : 꼭지점의 수
E : 모서리의 수
F : 면의 수
평면으로 이루어진 다면체에서는 V-E+F=2 가 성립한다.
증명
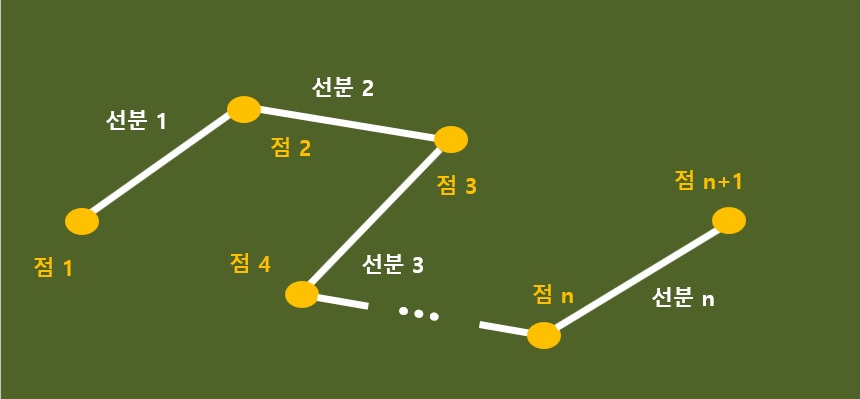
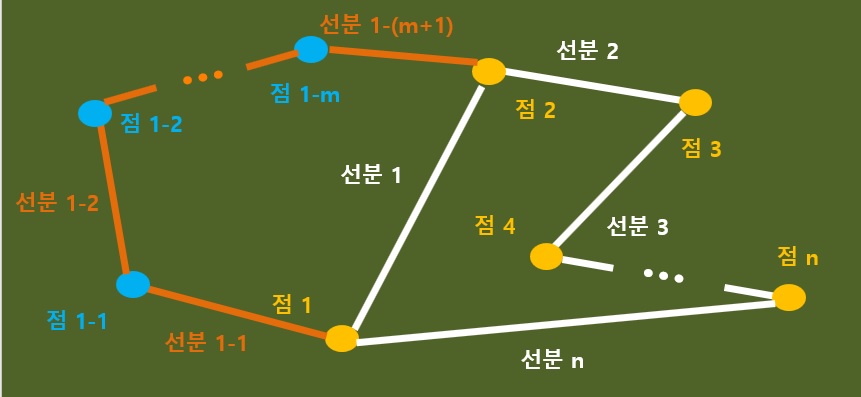
이 때 오일러 표수를 알아보자. 오일러 표수의 이전과 차이가 없다
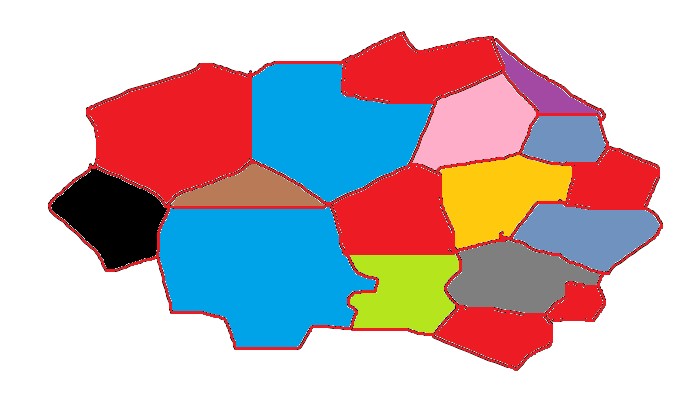
저런 면을 점과 선, 면의 갯수 변화 없이 저런 바구니 형태로 만들 수 있다
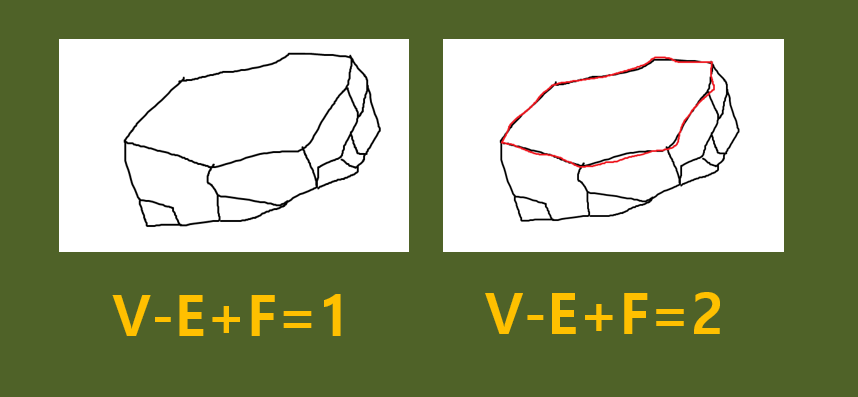
바구니에 뚜껑을 얹어놓으면 오일러 표수가 1에서 2가 된다
자세한 내용은 아래 영상을 보시고 참고하시면 되겠습니다.